本文共 3585 字,大约阅读时间需要 11 分钟。
一、IE和Chrome等浏览器与zoom
还在几年前,zoom还只是IE浏览器自己私有的玩具,但是,现在,除了FireFox浏览器,其他,尤其Chrome和移动端浏览器已经很好支持zoom属性了:
如下:
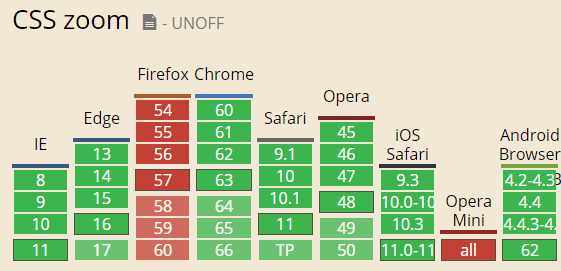
zoom的字面意思是“变焦”,摄影的时候常用到的一个概念。对于web上的zoom效果,你也可以按照此概念理解。可以改变页面上元素的尺寸,属于真实尺寸。
在旧的web时代。*zoom: 1可以给IE6/IE7浏览器增加haslayout, 用来清除浮动,修复一些布局上的疑难杂症等。
其支持的值类型有:
- 百分比值:
zoom:50%,表示缩小到原来的一半。 - 数值:
zoom:0.5,表示缩小到原来的一半。 - normal关键字:
zoom:normal等同于zoom:1.
注意,虽然Chrome/Safari浏览器支持了zoom属性,但是,其实zoom并不是标准属性。
二、CSS3 transform下的scale
而transform下的scale就不一样了,是明明确确写入规范的。从IE9+到其他现代浏览器都支持。语法为:transform: scale(<x> [<y>]). 同时有scaleX, scaleY专门的x, y方向的控制。
和zoom不同,scale并不支持百分比值和normal关键字,只能是数值。而且,还能是负数,没错,负数。而zoom不能是负值!
三、zoom和scale更深层次的差异
先总结下上面表面所见的差异:
- 浏览器兼容性。IE全族/Chrome/Safari和IE9+现代浏览器的差别。
- 控制缩放的值不一样。
zoom更全面,但是不能是负数,只能等比例控制;而scale虽然只能是数值,但是能负数,可以只控制1个维度。
然而,更深层次的差异才是更重要的。
您可以狠狠地点击这里:
从demo我们看出如下几点差异:
- zoom的缩放是相对于左上角的;而scale默认是居中缩放;
- zoom的缩放改变了元素占据的空间大小;而scale的缩放占据的原始尺寸不变,页面布局不会发生变化;
- zoom和scale对元素的渲染计算方法可能有差异(如下截图示意)。
更新于2018-01-09
今天又测了下,发现Chrome浏览器下已经几乎看不出两者渲染差异了。此tips作废。 - 对文字的缩放规则不一致。zoom缩放依然受限于最小12像素中文大小限制;而scale就是纯粹的对图形进行比例控制,文字50%原来尺寸。

然后,还有一个肉眼看不见却更重要的差异,渲染的性能差异明显。
由于zoom的缩放会改变元素的真实空间大小,换句话说,实时影响了其他小伙伴。
根据我的一些同事的测试,在文档流中zoom加在任意一个元素上都会引起一整个页面的重新渲染,而scale只是在当前的元素上重绘。这其实很好理解,对吧。scale呢变化时候,其原本的尺寸是不变的,因此,就没有layout的重计算;但是zoom牵一发动全身,就麻烦地多!
这就让我们要斟酌下移动端一些功能的实现了。
我们要实现元素的缩放效果,可以使用CSS3 animation, 但是存在这样一种情况,就是元素原本就使用了一些transform属性进行,此时,再使用scale进行animation缩放,就会覆盖原来的值,事情就会变得麻烦。
聪明的小伙伴想到了一个方法,就是使用zoom做动画。从效果上讲,zoom是可以的;但是,从性能上讲,大家就要掂量掂量了,不要弄好后,发现某些Android机子下面动画就像便秘一样,屎拉了一半悬着就是掉不下来,你就有的搞了。
我能说的就这么多,其他靠你自己了!![]()
四、结束语
今年的QQ公众号项目就有使用zoom/scale, 实现图片hover放大的效果.IE7/IE8使用zoom, 其他浏览器使用CSS3 transform scale值实现。至于zoom缩放不是按照中心点缩放的这个兼容性差异,通过使用「海洋布局」实现,具体可参考“”一文,其中就有兼容使用zoom/scale的例子。
在移动端,大家也可以使用zoom进行一些静态内容的控制,可以避免为了scale而占有translate, rotate, skew等公用的transform属性。
需要注意的是,Chrome等浏览器下,zoom/scale不要同时使用,因为,缩放效果会累加。如下图所示的4倍变小:

一、IE和Chrome等浏览器与zoom
还在几年前,zoom还只是IE浏览器自己私有的玩具,但是,现在,除了FireFox浏览器,其他,尤其Chrome和移动端浏览器已经很好支持zoom属性了:
如下:

zoom的字面意思是“变焦”,摄影的时候常用到的一个概念。对于web上的zoom效果,你也可以按照此概念理解。可以改变页面上元素的尺寸,属于真实尺寸。
在旧的web时代。*zoom: 1可以给IE6/IE7浏览器增加haslayout, 用来清除浮动,修复一些布局上的疑难杂症等。
其支持的值类型有:
- 百分比值:
zoom:50%,表示缩小到原来的一半。 - 数值:
zoom:0.5,表示缩小到原来的一半。 - normal关键字:
zoom:normal等同于zoom:1.
注意,虽然Chrome/Safari浏览器支持了zoom属性,但是,其实zoom并不是标准属性。
二、CSS3 transform下的scale
而transform下的scale就不一样了,是明明确确写入规范的。从IE9+到其他现代浏览器都支持。语法为:transform: scale(<x> [<y>]). 同时有scaleX, scaleY专门的x, y方向的控制。
和zoom不同,scale并不支持百分比值和normal关键字,只能是数值。而且,还能是负数,没错,负数。而zoom不能是负值!
三、zoom和scale更深层次的差异
先总结下上面表面所见的差异:
- 浏览器兼容性。IE全族/Chrome/Safari和IE9+现代浏览器的差别。
- 控制缩放的值不一样。
zoom更全面,但是不能是负数,只能等比例控制;而scale虽然只能是数值,但是能负数,可以只控制1个维度。
然而,更深层次的差异才是更重要的。
您可以狠狠地点击这里:
从demo我们看出如下几点差异:
- zoom的缩放是相对于左上角的;而scale默认是居中缩放;
- zoom的缩放改变了元素占据的空间大小;而scale的缩放占据的原始尺寸不变,页面布局不会发生变化;
- zoom和scale对元素的渲染计算方法可能有差异(如下截图示意)。
更新于2018-01-09
今天又测了下,发现Chrome浏览器下已经几乎看不出两者渲染差异了。此tips作废。 - 对文字的缩放规则不一致。zoom缩放依然受限于最小12像素中文大小限制;而scale就是纯粹的对图形进行比例控制,文字50%原来尺寸。

然后,还有一个肉眼看不见却更重要的差异,渲染的性能差异明显。
由于zoom的缩放会改变元素的真实空间大小,换句话说,实时影响了其他小伙伴。
根据我的一些同事的测试,在文档流中zoom加在任意一个元素上都会引起一整个页面的重新渲染,而scale只是在当前的元素上重绘。这其实很好理解,对吧。scale呢变化时候,其原本的尺寸是不变的,因此,就没有layout的重计算;但是zoom牵一发动全身,就麻烦地多!
这就让我们要斟酌下移动端一些功能的实现了。
我们要实现元素的缩放效果,可以使用CSS3 animation, 但是存在这样一种情况,就是元素原本就使用了一些transform属性进行,此时,再使用scale进行animation缩放,就会覆盖原来的值,事情就会变得麻烦。
聪明的小伙伴想到了一个方法,就是使用zoom做动画。从效果上讲,zoom是可以的;但是,从性能上讲,大家就要掂量掂量了,不要弄好后,发现某些Android机子下面动画就像便秘一样,屎拉了一半悬着就是掉不下来,你就有的搞了。
我能说的就这么多,其他靠你自己了!![]()
四、结束语
今年的QQ公众号项目就有使用zoom/scale, 实现图片hover放大的效果.IE7/IE8使用zoom, 其他浏览器使用CSS3 transform scale值实现。至于zoom缩放不是按照中心点缩放的这个兼容性差异,通过使用「海洋布局」实现,具体可参考“”一文,其中就有兼容使用zoom/scale的例子。
在移动端,大家也可以使用zoom进行一些静态内容的控制,可以避免为了scale而占有translate, rotate, skew等公用的transform属性。
需要注意的是,Chrome等浏览器下,zoom/scale不要同时使用,因为,缩放效果会累加。如下图所示的4倍变小:

转载地址:http://czvwz.baihongyu.com/